



suivant: Traitement du signal Création
monter: SOUTENANCE FINALE MARVIN (Modest-encoding
précédent: Le projet
Table des matières
Sous-sections
Cette partie expose le fonctionnement du système de vérification du locuteur de MARVIN.
Outre la présentation du schéma général et de la sélection des empreintes vocales
nous développerons également l'étude, l'implémentation et les premiers tests
de notre structure d'apprentissage. Celle-ci est basée sur
les réseaux de neurones, une technique peu courante en vérification
du locuteur bien que ceux-ci présentent des caractéristiques très
intéressantes leur permettant de fonctionner en traitement du signal.
Nous nous sommes intéressé dans un premier temps aux réseaux de
neurones de type perceptron multi-couches, l'élaboration de celui-ci n'a
pas posé de problèmes particuliers (du fait des nombreuses documentation
existant à son sujet) mais lors de la phase de test ceux-ci se sont révélés
peu performant nous avons donc dû développer un autre type de réseau de neurone
le TDNN (Time Delay Neural Network ou réseau à convolution) qui, comme nous le verrons
par la suite possède d'intéressantes propriétés de robustesse vis-à-vis en particulier de la translation. Mais l'implémentation du TDNN a posé de nombreux problèmes du fait de la difficulté de trouver des informations sur celui-ci.
La suite de cette partie présente les différentes optimisations que nous avons effectué sur le TDNN et l'inter-opérabilité C/CAML.
![\includegraphics[]{apprentissage.ps}](img1.png)
![\includegraphics[]{recognition.ps}](img2.png)
Afin de pouvoir procéder par la suite à une reconnaissance efficace nous devons avant tout "apprendre" des échantillons de voix "justes".
En effet, lors de l'enregistrement il est possible qu'il y ait une perturbation, un bruit de fond rendant cet échantillon de voix faux.
Il nous est donc rapidement apparut la nécessité de mettre au point un mécanisme de sélection des empreintes vocales qui seront
apprises par le réseau de neurone.
Nous avons dans un premier lieu recherché des algorithmes servant à la classification tel la LVQ
(Linear Vector Quantization) mais nous nous sommes rapidement rendu compte que de telles méthodes n'étaient pas nécessaires pour un
problème aussi simple. En effet nous devons avant tout reconnaître une forme aussi simplement que possible et l'une des méthodes que nous avons développé en un premier temps est de baser cette reconnaissance sur les variations de l'empreinte. Cependant cette méthode nous a vite montré ses limites étant donné qu'elle ne prend pas compte les amplitudes.
Nous allons ci-après vous détailler le fonctionnement de celle-ci et présenter la nouvelle méthode de préselection adoptée.
Afin de détecter les variations nous devons concevoir un algorithme permettant de reconnaître un pic dans un signal.
Pour cela nous définissons les formes primitives :
![\includegraphics[height=2cm]{prim.ps}](img3.png)
Par la suite nous définissons un pic par les prédicats suivant :
- un pic est composé d'une partie ascendante, d'une partie horizontale (éventuellement nulle) et une partie descendante
- une partie ascendante est composée de lettres A parmi lesquelles on peut trouver une lettre C mais pas de lettre B
- une partie horizontale n'est composée que de C
- une partie descendante est composée de lettres B parmi lesquelles on peut trouver une lettre C mais pas de lettre A
Nous allons donc traduire notre empreinte vocale en un mot composé d'un alphabet de trois lettres dans lequel nous trouvons la grammaire suivante :
Par la suite le fonctionnement de l'algorithme est simple : après la traduction de toutes les empreintes vocales en mots nous sélectionnons le mot qui ressort le plus souvent comme étant la bonne empreinte.
![\includegraphics[height=10cm]{emp.ps}](img5.png) six empreintes du même sujet
six empreintes du même sujet
Dans les six empreintes suivantes nous souhaitons sélectionner les ``meilleures''. L'algorithme nous donne les résultats suivants :
- A B A B A B A B A B
- A B A B A B A B A B A B
- A B A B A B A B A B
- A B A B A B A B A B
- A B A B A B A B
- A B A B A B A B A B
Finalement les empreintes sélectionnées seront les empreintes 1, 3, 4 et 6 ce qui paraît cohérent.
La nouvelle méthode utilisée est basée sur l'utilisation du TDNN et de la reconnaissance des empreintes, cela constitue donc un système de sélection beaucoup plus proche des objectifs que nous nous étions fixé soit l'identification de l'empreinte. Son fonctionnement est simple : il s'agit pour chaque empreinte de créer le TDNN associé et de tester l'ensemble des empreintes avec ce réseau neuronal en notant les empreintes reconnues. Au final nous sélectionnons l'empreinte qui a en reconnu le plus ainsi que les empreintes reconnues.
Exemple : Soit un ensemble de dix empreintes 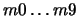
 reconnaît
reconnaît 
 reconnaît
reconnaît 
 ne reconnaît rien
ne reconnaît rien
 reconnaît
reconnaît

 reconnaît
reconnaît 
 reconnaît
reconnaît 
 ne reconnaît rien
ne reconnaît rien
 reconnaît
reconnaît 
 ne reconnaît rien
ne reconnaît rien
 reconnaît
reconnaît 
Nous sélectionnerons donc ici les empreintes
 .
Nous avons donc réussi à mettre au point un mécanisme simple nous permettant de sélectionner les empreintes les plus réussies. Par la suite nous calculons la moyenne des empreintes sélectionnées, celle-ci constituera l'empreinte générale qui servira à la création du TDNN.
Un réseau neuronal repose sur la notion de graphe; un graphe consiste en des noeuds représentant les agents, et des connexions représentant les interactions entre ces agents. Les connexions sont le plus souvent "plastiques", en ce sens que les poids liés à ces connexions sont modifiables. Ils consistent en des modèles plus ou moins inspirés du fonctionnement cérébral de l'être humain, en se basant particulièrement sur le concept de neurone. Un neurone est une cellule particulière possédant des extensions par lesquelles il peut distribuer des signaux (axones) ou en recevoir (dendrites).
Un perceptron multi-couches est un réseau formé de couches (i.e. groupe de neurones) avec une connectivité particulière, chaque couche est reliée à la suivante (chaque couches reliées entre elles ont une connectivité totale). Par exemple pour un réseau à trois couches la première est reliée à la deuxième qui est reliée à la troisième. La première couche s'appelle couche d'entrée, la dernière est nommée couche de sortie et les couches intermédiaires sont désignées par le terme de "couches cachées".
.
Nous avons donc réussi à mettre au point un mécanisme simple nous permettant de sélectionner les empreintes les plus réussies. Par la suite nous calculons la moyenne des empreintes sélectionnées, celle-ci constituera l'empreinte générale qui servira à la création du TDNN.
Un réseau neuronal repose sur la notion de graphe; un graphe consiste en des noeuds représentant les agents, et des connexions représentant les interactions entre ces agents. Les connexions sont le plus souvent "plastiques", en ce sens que les poids liés à ces connexions sont modifiables. Ils consistent en des modèles plus ou moins inspirés du fonctionnement cérébral de l'être humain, en se basant particulièrement sur le concept de neurone. Un neurone est une cellule particulière possédant des extensions par lesquelles il peut distribuer des signaux (axones) ou en recevoir (dendrites).
Un perceptron multi-couches est un réseau formé de couches (i.e. groupe de neurones) avec une connectivité particulière, chaque couche est reliée à la suivante (chaque couches reliées entre elles ont une connectivité totale). Par exemple pour un réseau à trois couches la première est reliée à la deuxième qui est reliée à la troisième. La première couche s'appelle couche d'entrée, la dernière est nommée couche de sortie et les couches intermédiaires sont désignées par le terme de "couches cachées".
On définit un perceptron multi-couches par :
- Une fonction de transfert
 , commune à tout les neurones. Celle-ci est une fonction sigmoïdale (par exemple
, commune à tout les neurones. Celle-ci est une fonction sigmoïdale (par exemple  ou
ou
 );
);
- Les poids des connexions
 , relatifs à la connexion entre le neurone
, relatifs à la connexion entre le neurone  et le neurone
et le neurone  . Le signal à la sortie de
. Le signal à la sortie de  sera multiplié par ce poids avant d'arriver à l'entrée de
sera multiplié par ce poids avant d'arriver à l'entrée de  ;
;
- Le seuil
 , relatif au neurone
, relatif au neurone  ;
;
- L'activation du neurone en sortie
 , relatif au neurone
, relatif au neurone  . Cette activation est égale à
. Cette activation est égale à
 ;
;
L'apprentissage dans un perceptron multi-couches est de type supervisé c'est à dire que l'on procède par correction d'erreur (i.e. nous "donnons" au réseau un vecteur d'entrée, le propageons puis calculons l'erreur en sortie par rapport à un vecteur de "sorties désirées" afin de modifier les poids en fonction de cette erreur).
L'apprentissage dans un perceptron peut donc se décomposer en quatre phases :
- La propagation du signal de la couche d'entrée jusqu'à la couche de sortie;
- Le calcul de l'erreur en sortie;
- La rétro propagation de l'erreur;
- Correction des poids;
L'apprentissage va donc consister en une minimisation d'une fonction d'erreur en utilisant l'algorithme de rétro-propagation de l'erreur qui repose sur une minimisation par descente de gradient d'un critère d'erreur de type moindres-carrés.
Pour cette partie, de nouvelles notations s'imposent :
- L'ensemble
 des exemples d'apprentissage (i.e. ensemble des vecteurs d'entrée et les vecteur de sorties désirées correspondants);
des exemples d'apprentissage (i.e. ensemble des vecteurs d'entrée et les vecteur de sorties désirées correspondants);
- L'ensemble
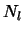 des neurones de sortie de la couche
des neurones de sortie de la couche  ;
;
 l'activation du neurone de sortie
l'activation du neurone de sortie  pour l'exemple
pour l'exemple  ;
;
 est la valeur de sortie désirée pour le neurone
est la valeur de sortie désirée pour le neurone  avec l'exemple
avec l'exemple  ;
;
 est l'activité présente à l'entrée du neurone
est l'activité présente à l'entrée du neurone  pour l'exemple
pour l'exemple  ;
;
 est le pas d'apprentissage;
est le pas d'apprentissage;
Soit  le vecteur des signaux d'entrée du réseau et
le vecteur des signaux d'entrée du réseau et  le vecteur des signaux de sortie. La phase de propagation est assez simple car il s'agit simplement de remplacer les activations des neurones d'entrée par les valeur de
le vecteur des signaux de sortie. La phase de propagation est assez simple car il s'agit simplement de remplacer les activations des neurones d'entrée par les valeur de  puis de propager le signal en procédant couches par couches. Par exemple, pour un réseau à 2 couches cachées, les valeurs du vecteur des signaux de sortie
puis de propager le signal en procédant couches par couches. Par exemple, pour un réseau à 2 couches cachées, les valeurs du vecteur des signaux de sortie  sont égales à :
sont égales à :
avec  la fonction de transfert du réseau et
la fonction de transfert du réseau et  la matrice de connexion reliant la couche
la matrice de connexion reliant la couche  à la couche
à la couche  .
L'erreur en sortie correspond à une fonction de coût notée C (fonction d'erreur), que l'on doit minimiser au cours de l'apprentissage. Posons ici la fonction appelée critère des moindres-carrés :
.
L'erreur en sortie correspond à une fonction de coût notée C (fonction d'erreur), que l'on doit minimiser au cours de l'apprentissage. Posons ici la fonction appelée critère des moindres-carrés :
Cette fonction d'erreur n'est pas la seule possible, toute fonction dérivable en  et
et  est valable.
Un des points important dans la conception d'une application à base de réseaux de neurones concerne la méthode d'apprentissage. Celle-ci doit idéalement nous permettre de converger rapidement vers le minimum global de la fonction de coût choisie. Cependant les méthodes permettant de trouver le minimum global d'une fonction sont en général très lentes en considérant le nombre de paramètres que nous devrons prendre en compte. Nous avons donc utilisé l'algorithme de rétro-propagation du gradient qui ne garantit pas d'aboutir au minimum global de la fonction
est valable.
Un des points important dans la conception d'une application à base de réseaux de neurones concerne la méthode d'apprentissage. Celle-ci doit idéalement nous permettre de converger rapidement vers le minimum global de la fonction de coût choisie. Cependant les méthodes permettant de trouver le minimum global d'une fonction sont en général très lentes en considérant le nombre de paramètres que nous devrons prendre en compte. Nous avons donc utilisé l'algorithme de rétro-propagation du gradient qui ne garantit pas d'aboutir au minimum global de la fonction  , mais celui-ci est beaucoup plus rapide et est donc utilisable dans le cadre de notre application.
, mais celui-ci est beaucoup plus rapide et est donc utilisable dans le cadre de notre application.
Le but de l'algorithme de rétro-propagation du gradient est de minimiser notre fonction de coût (i.e. de minimiser l'erreur). Pour cela il utilise le concept de dérivées partielles et calcule le gradient de la fonction de coût qui fournit une indication sur la direction et l'amplitude du changement à effectuer sur les poids  pour minimiser
pour minimiser  . En effet cet algorithme utilise le fait qu'en tout point le gradient est normal aux lignes de niveau ce qui permet de connaître la direction d'un des minimum de
. En effet cet algorithme utilise le fait qu'en tout point le gradient est normal aux lignes de niveau ce qui permet de connaître la direction d'un des minimum de  .
.
La modification des poids suivra donc une loi du type :
La complexité de cet algorithme est donc fonction du nombre de paramètres (poids) à traiter et augmente très vite avec la taille du réseau neuronal.
L'algorithme se décompose donc en quatre phases :
On note le gradient
On a vu plus haut que
or
avec
On pose le terme d'erreur
finalement
Ceci est la forme générale de la correction d'erreur à effectuer quelque soit la couche. Cependant le terme d'erreur varie selon que nous soyons sur la dernière couche ou sur une des couches cachées.
Ce terme d'erreur  peut être obtenu récursivement par rétro-propagation.
peut être obtenu récursivement par rétro-propagation.
- Dernière couche
Pour le rétro-propagation de l'erreur la valeur initiale de l'erreur peut être obtenue ainsi :
- Puis récursivement (pour les couches cachées)
soit
or
finalement
- Correction des poids
On peut effectuer la modification des poids selon plusieurs méthodes, les deux principales diffèrent selon la manière de calculer le gradient, soit en utilisant le gradient total c'est à dire que l'on modifie les poids une fois l'ensemble des exemples  traités (on somme les modifications durant tout l'apprentissage de
traités (on somme les modifications durant tout l'apprentissage de  puis on met a jour les poids à la fin d'une époque). L'autre méthode qui est appelée la rétro-propagation du gradient stochastique utilise un gradient partiel c'est à dire que les modifications de poids se font au fur et à mesure de l'apprentissage (après chaque propagation d'un exemple on modifie les poids).
Un patron est un vecteur qui englobe l'ensemble des exemples d'apprentissage.
puis on met a jour les poids à la fin d'une époque). L'autre méthode qui est appelée la rétro-propagation du gradient stochastique utilise un gradient partiel c'est à dire que les modifications de poids se font au fur et à mesure de l'apprentissage (après chaque propagation d'un exemple on modifie les poids).
Un patron est un vecteur qui englobe l'ensemble des exemples d'apprentissage.
Un corpus est un ensemble d'apprentissage il contient plusieurs patrons comportant les vecteurs d'entrée et les vecteurs de sorties désirées correspondants.
/* Pour les patrons */
typedef struct
{
double *donnees;
int nombre, largeur;
/* La largeur est utilisée afin de retrouver le nième patron */
} t_patrons;
/* Pour les corpus */
typedef struct
{
int nombre_patrons;
t_patrons entrees, sorties_desirees;
} t_corpus;
/* Pour les couches */
typedef struct
{
int nombre_neurones;
int premier_neurone;
} t_couche_neurones;
/* Pour les réseaux */
typedef struct
{
/* Neurones */
int nombre_neurones;
double *activation;
double *activation_ponderee;
double *erreur;
double *erreur_ponderee;
double *entree;
double *sortie_desiree;
/* Liens */
int nombre_liens;
double *poids;
/* Couches de Neurones */
int nombre_couches;
t_couche_neurones *couches;
} t_reseau;
Dans un premier temps le PMC a été conçu avec un type de donnée hétérogène (de type structure lourde avec pointeurs et allocations). Celui-ci marchait mais était très lent, nous l'avons donc modifié et recodé entièrement en ce que nous pourrions appeler une structure homogène (la structure utilisée la plus lourde est le vecteur). L'apprentissage consiste donc uniquement en une modification d'un tableau de liens et de seuils. La vitesse en a été considérablement augmentée.
Lors des premiers test nous avons testé l'apprentissage d'une fonction de type sinus entre 0 et 1 en lui donnant en entrée uniquement 500 exemples de cette fonction dans l'intervalle donné. Nous avons réussi avec un réseau de type [1,20,20,1] à obtenir une approximation de la fonction à 0.02 près.
Cependant lors du test de l'apprentissage d'une empreinte vocale le système reconnaît très bien l'empreinte de base qui a servi à l'apprentissage mais il suffisait de décaler le signal pour que les résultats soient faux.
L'utilisation du perceptron multi-couches classique dans le cadre de l'identification d'un signal paraît donc proscrite, et nous impose donc une structure plus évoluée évoquée précédement le Time Delay Neural Network (TDNN). Cette structure devra prendre en compte une notion de temps afin de pouvoir être adaptée à l'apprentissage d'un signal vocal.
Nous avons donc dû rechercher un type de réseau de neurone qui pouvait correspondre à nos contraintes : une robustesse vis-à-vis de la translation mais aussi une capacité de généralisation. Lors de nos recherches au début de l'année nous avions déjà rencontré ce type de réseau de neurones en particulier dans la thèse de Benani (1992). Les TDNN ont été développé à l'origine dans le cadre de la reconnaissance de phonème (Lang et Hinton 1988 ; Waibel 1989) mais ont été depuis adaptés à la reconnaissance vocale (Bottou 1990) et à la reconnaissance de l'écriture manuscrite (Guyon 1991).
Le TDNN se singularise d'un perceptron multi-couches classique par le fait qu'il prend en compte une certaine notion de temps. C'est à dire qu'au lieu de prendre en compte tous les neurones de la couche d'entrée en même temps il va effectuer un balayage temporel. La couche d'entrée du TDNN prend une fenêtre du spectre et balaye l'empreinte. Le TDNN permet ainsi de reconnaître le signal tout en étant moins strict que le PMC classique (c'est à dire qu'il pourra y avoir des petits décalages).
Les TDNN sont constitués comme les PMC d'une couche d'entrée, de couches cachées et d'une couches de sortie mais ils se différencie de part l'organisation des liaisons inter-couches. Les TDNN introduisent des contraintes qui leurs permettent d'avoir un certain degré d'invariance par décalage temporel et déformation. Celles-ci utilisent trois idées : poids partagés, fenêtre temporelle et délai.
- Les poids partagés permettent de réduire le nombre de paramètres du réseau neuronal et induisent ainsi une capacité de généralisation plus importante. Les poids sont partagés suivant la direction temporelle, c'est à dire que pour une caractéristique donnée, la fenêtre associée à celle-ci aura les mêmes poids selon la direction temporelle. De plus cette contrainte entraîne une capacité d'extraire les différences au fur et à mesure du balayage du signal. Ce concept de poids partagés est le comportement présumé du cerveau humain ou plusieurs neurones calculent la même fonction sur des entrées différentes.
- Le concept de fenêtre temporelle implique que chaque neurone de la couche l+1 n'est connecté qu'à un sous ensemble de la couche l (nous n'avons plus une connectivité totale). La taille de cette fenêtre est la même entre deux couches données. Cette fenêtre temporelle permet que chaque neurone n'ait qu'une vision locale du signal, il peut être vu comme une unité de détection d'une caractéristique locale du signal.
- En plus des deux contraintes précédente nous introduisons des délais entre deux fenêtre successive pour une couche donnée.
De plus chaque couche a deux direction : une direction temporelle et une direction caractéristique.
Le but du TDNN est non pas d'apprendre basiquement le signal mais d'extraire les caractéristique de celui-ci. La première couche acquière le signal puis une ou plusieurs couches cachées transforment le signal en des vecteurs de caractéristiques. Un neurone donné détecte une caractéristique locale de la variation de la courbe. Le champ de vision du neurone est restreint à une fenêtre temporelle limitée. Avec la contrainte des poids partagés, le même neurone est dupliqué dans la direction temps (la même matrice de poids dupliquée) pour détecter la présence ou l'absence de la même caractéristique à différentes places le long du signal. En utilisant plusieurs neurones à chaque position temporelle, le réseau de neurone effectue la détection de caractéristiques différentes : les sorties des différents neurones produisent un nouveau vecteur caractéristique pour la couche supérieure.
La composante temporelle du signal d'origine est peu à peu éliminée au fur et à mesure de sa transformation en caractéristique par les couches supérieures, pour compenser cette perte d'information on augmente le nombre de neurones dans la direction caractéristique.
Pour l'apprentissage du TDNN nous utilisons le classique algorithme de rétro-propagation du gradient mais dans sa version stochastique (c'est à dire que les poids sont mis à jour à chaque exemple). Les phases de calcul sont les mêmes que celle décrites précédemment.
Ayant besoin de faire un certain nombre de test pour déterminer la topologie qui sera la plus adaptée à notre application nous avons eu besoin, comme pour le perceptron multi-couches, de développer non pas un réseau neuronal particulier mais un simulateur neuronal nous permettant de le modeler à loisir. Nous avons suivi le même mode de conception que pour le PMC, mais nous avons rencontré des difficultés pour la rétro-propagation de l'erreur, plus subtile que dans le PMC.
Pour l'implémentation en elle même, nous avons utilisé un pas de  , initialisé les biais et les poids à des valeurs entre
, initialisé les biais et les poids à des valeurs entre  et
et  .
Le type TDNN se caractérise par :
.
Le type TDNN se caractérise par :
- Le nombre de couches nb_layers
- Le nombre de neurones de chaque couches selon la direction temporelle, window_t
- Le nombre de neurones de chaque couches selon la direction caractéristique nb_feat
- La taille de la fenêtre temporelle vue par chaque couche (sauf celle d'entrée), le nombre de neurones de la couche l vu par un neurone de la couche l+1, field_t
- Le délai temporel (nombre de neurones) entre chaque fenêtre, delay
Un neurone est caractérisé par sa couche l, sa caractéristique f, et son emplacement temporel t.
- x[t][f] activation en sortie du neurone
- w[f][f(couche-1)][t] matrice des poids
- w_biais[f] poids des biais
- sum[t][f] somme des entrées
- e[t][f] terme d'erreur
- delta[f][f(couche-1)][t] le gradient
#define MAXTEMP 12
#define MAXFEAT 8
#define MAXFIELD 5
#define MAXLAYERS 3
#define MAXDELAY 1
typedef struct s_neuron
{
float x[MAXTEMP][MAXFEAT];
float d[MAXTEMP][MAXFEAT];
// float w[MAXFEAT][MAXFEAT][MAXFIELD];
float ***w;
float w_biais[MAXFEAT];
float sum[MAXTEMP][MAXFEAT];
float e[MAXTEMP][MAXFEAT];
// float delta[MAXFEAT][MAXFEAT][MAXFIELD];
float ***delta;
} t_neuron;
typedef struct s_layer
{
int window_t;
int nb_feat;
int field_t;
int delay;
t_neuron *neurons;
} t_layer;
typedef struct s_tdnn
{
int nb_layers;
t_layer **layers;
} t_tdnn;
typedef struct s_patrons
{
float *donnees;
int nombre, largeur;
} t_patrons;
typedef struct s_corpus
{
int nombre_patrons;
t_patrons entrees, sorties_desirees, test;
} t_corpus;
La topologie sur laquelle nous nous sommes arrêtés, pour l'instant, est :
- nb_layers = 3 (une couche cachée)
- Couche d'entrée window_t = 12, nb_feat = 1
- Couche cachée window_t = 10, nb_feat = 8, field_t = 3, delay = 1
- Couche de sortie window_t = 6, nb_feat = 2, field_t = 5, delay = 1
Nous n'avons fait pour l'instant que quelques tests, mais ceux-ci paraissent encourageant et donnent d'assez bon résultats.
Nous disposons maintenant d'une structure d'apprentissage qui correspond aux critères que nous nous étions fixé dans le cahier des charges. Je profiterais à présent de l'avance que j'ai dans le planning pour mettre au point une méthode permettant d'adapter le pas d'apprentissage au fur et à mesure de celui-ci et pour faire d'autres recherches sous MatLab afin d'optimiser notre post-traitement.
L'implémentation du TDNN en C a posé de nombreux problèmes au niveau des tests d'architectures. En effet les erreurs tels que les débordements de tableau ne sont pas gérées en langage C ce qui nous a amené à de nombreuses difficultés tels que des bogues ne se révélant qu'en produisant des résultats incohérents. Afin de pouvoir tester différentes architectures de TDNN en toute ``sécurité'' (nous voulons dire par là que les propagations et rétropropagation sont justes) nous avons recodé le TDNN entièrement en CAML. CAML offre au niveau de la gestion des gros tableau multidimensionnels des fonctions très pratiques, de plus CAML ne laisse passer aucune erreur de débordement.
Nous avons eu de nombreuses difficultées lors de cette traduction/correction du C vers le CAML. En effet nous avons dû mélanger deux styles de programmation : la programmation impérative et récursive. La puissance du langage CAML nous a néanmoins agréablement surpris nous offrant, grâce à la programmation par objet, un environnement de simulation du TDNN très abouti. De plus les possibilités d'interfacage entre C et CAML nous permettrons d'intégrer directement notre code CAML dans notre code C.
Le TDNN est considéré comme un objet ce qui permet une gestion de celui-ci beaucoup plus rapide.
class tdnn (nb_couches_i,nb_t_i,nb_c_i,fenetre_t_i,delai_i,entrees_i,sorties_i,
sigmoide_i,derivee_i) = object
val nb_couches = nb_couches_i
val nb_t = nb_t_i
val nb_c = nb_c_i
val fenetre_t = fenetre_t_i
val delai = delai_i
val entrees = entrees_i
val sorties = sorties_i
val mutable activation = [|[|[||]|]|]
val mutable poids = [|[|[|[||]|]|]|]
val mutable somme = [|[|[||]|]|]
val mutable erreur = [|[|[||]|]|]
val mutable gradient = [|[|[|[||]|]|]|]
val sigmoide = sigmoide_i
val derivee = derivee_i
method init = activation <- init_tri (nb_couches,nb_t,nb_c);
somme <- init_tri (nb_couches,nb_t,nb_c);
erreur <- init_tri (nb_couches,nb_t,nb_c);
poids <- init_qua (nb_couches,nb_c,fenetre_t);
gradient <- init_qua (nb_couches,nb_c,fenetre_t);
method rand_poids = f_rand_poids(poids)
method donner_activation n = f_donner_activation (activation,entrees,n,
List.nth nb_t 0,List.nth nb_c 0)
method propager_activation = f_propager_activation (activation,somme,poids,nb_c,
fenetre_t,delai,sigmoide)
method calculer_erreur_sortie n = f_calculer_erreur_sortie (erreur,activation,
sorties,n)
method calculer_gradient eta = f_calculer_gradient (erreur,activation,somme,
poids,eta,delai,derivee,
nb_couches,nb_c,fenetre_t)
method get_erreur_reseau = f_erreur_reseau (erreur)
method get_nb_couches = nb_couches
method get_activation = activation
method get_somme = somme
method get_poids = poids
method get_nb_t = nb_t
method get_nb_c = nb_c
method get_fenetre_t = fenetre_t
method get_delai = delai
method get_sigmoide = sigmoide
method get_erreur = erreur
method get_gradient = gradient
method get_entrees = entrees
end;;
Ainsi un apprentissage se résume ensuite simplement à la suite de commandes :
network#init;;
network#rand_poids;;
epoque(network,100000,0.01);;
Afin de pouvoir utiliser le TDNN créé en CAML à partir de C (i.e. pouvoir appeller les différentes fonctions d'apprentissage et de reconnaissance) nous avons dû créer une 'interface' entre les deux langages. En effet nous avons été exposé à de nombreuses difficultées dont la plus importante était le passage de paramètres de C à CAML et vice versa. Mais CAML dispose d'énormement de fonctions de conversions entre les deux types de gestion de mémoire.
Finalement cette implémentation du TDNN en CAML, loin d'être une perte de temps, s'est révélée très précieuse à l'évolution de Marvin car en plus d'une belle expérience de la puissance du langage CAML il nous a permis de concevoir un environnement d'expérimentation pour l'apprentissage des empreintes vocales très agréable à utiliser et beaucoup plus sûr.
Afin d'améliorer l'apprentissage nous avions exposé dans le dernier rapport la nécessité de mettre au point une méthode permettant de réguler le pas d'apprentissage au fur et à mesure de celui-ci ce qui aurait comme conséquence des résultats encore meilleurs et plus rapidement (en effet nous pouvons commencer avec un pas élevé et le baisser quand le besoin s'en fait ressentir). Dans cet objectif plusieurs méthodes ont été imaginées et mises en oeuvre, nous allons vous les présenter ci-dessous.
Dans un premier temps nous avions pensé à faire baisser le pas d'apprentissage à chaque fois que l'erreur en sortie du réseau neuronal remontait. Cependant lors des tests il nous est vite apparut que cette méthode n'était pas appliquable à notre problème. En effet, la phase d'apprentissage d'un réseau neuronal passe souvent par des phases de tâtonnement dans lesquelles le réseau neuronal ``désapprend'' avant de retomber dans une descente de l'erreur meilleure qu'auparavent (on sort en quelques sorte d'un minimum local). En appliquant cette méthode le pas diminuait donc à chaque fois que le réseau neuronal ``tâtonnait'' supprimant ou ralentissant donc cette phase bénéfique pour l'apprentissage.
Finalement nous devions trouver une méthode de contrôle du pas qui répondait à plusieurs contraintes :
- Tant que l'erreur est encore haute nous autorisons un grand nombre de tâtonnements avec un pas élevé, le réseau sera appelé instable
- Plus le temps d'apprentissage augmente (et parallèlement plus l'erreur baisse, en théorie) moins nous autorisons les augmentations de l'erreur, le réseau sera gelé
Nous devions donc concevoir une modification de pas prenant en compte le temps d'apprentissage et l'erreur, permettant de beaucoup tâtonner au début de l'apprentissage et d'affiner au maximum à la fin de celui-ci. Il nous est alors revenu en mémoire un principe que le cour de Micro-informatique de Sup nous avait présenté et qui correspond parfaitement aux contraintes que nous nous sommes posés : le recuit simulé.
Le principe du recuit simulé repose sur une analogie avec la thermodynamique qui a été révélée par les travaux simultanés de S. Kirkpatrick, C.D. Gelatt Jr. M.P. Vecchi et d'autre part par V. Cerny vers 1982 à partir de la méthode de Métropolis (1953). Il repose sur le fait qu'une dégradation provisoire peut entraîner une amélioration plus tard. On peut donc autoriser une transformation locale provoquant une augmentation de la fonction d'erreur avec une certaine probabilité.
L'état d'un matériau dépend de la température à laquelle il est porté, or la distribution de Gibbs-Boltzmann mesure la probabilité  de visiter l'état
de visiter l'état  en fonction de son énergie
en fonction de son énergie  et de la température
et de la température  (
( est la constante de Boltzmann et
est la constante de Boltzmann et 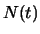 la fonction de partition) :
la fonction de partition) :

On peut observer que pour  fixé, un état est d'autant plus probable que son énergie est faible. De plus, si
fixé, un état est d'autant plus probable que son énergie est faible. De plus, si  est élevé par rapport à
est élevé par rapport à  la probabilité d'observer un état donné sera à peu près la même quel que soit l'état. A l'inverse si
la probabilité d'observer un état donné sera à peu près la même quel que soit l'état. A l'inverse si  est faible les états de faible énergie deviendront plus probables et à température presque nulle seuls les états à énergie nulle ont une probabilité non négligeable d'être observés.
Ces propriétés sont utilisées en métallurgie afin de produire des cristaux qui ont une configuration d'énergie minimum. En effet si on veut obtenir un cristal, i.e. un état d'énergie minimum, il faut faire décroître très lentement la température de telle sorte que l'équilibre thermique ait le temps de s'instaurer entre deux décroissances de température. Comme on ne dispose pas d'un temps infini, on fait décroître la température plus rapidement au risque d'obtenir des structures presque cristallines, mais présentant des défauts. Pour arriver à un état de cristal on réchauffe le matériau ce qui permet aux molécules d'effectuer des mouvements ce qui était interdit lorsque le système était gelé. En particulier ces mouvements entraînent une augmentation de l'énergie qui permet par la suite de passer une barrière énergétique et ainsi trouver une configuration d'énergie minimum (nous passons en quelque sorte un minimum local de l'énergie).
est faible les états de faible énergie deviendront plus probables et à température presque nulle seuls les états à énergie nulle ont une probabilité non négligeable d'être observés.
Ces propriétés sont utilisées en métallurgie afin de produire des cristaux qui ont une configuration d'énergie minimum. En effet si on veut obtenir un cristal, i.e. un état d'énergie minimum, il faut faire décroître très lentement la température de telle sorte que l'équilibre thermique ait le temps de s'instaurer entre deux décroissances de température. Comme on ne dispose pas d'un temps infini, on fait décroître la température plus rapidement au risque d'obtenir des structures presque cristallines, mais présentant des défauts. Pour arriver à un état de cristal on réchauffe le matériau ce qui permet aux molécules d'effectuer des mouvements ce qui était interdit lorsque le système était gelé. En particulier ces mouvements entraînent une augmentation de l'énergie qui permet par la suite de passer une barrière énergétique et ainsi trouver une configuration d'énergie minimum (nous passons en quelque sorte un minimum local de l'énergie).
![\includegraphics[height=5cm]{recuit.ps}](img85.png)
Nous allons donc utiliser le fait qu'une dégradation provisoire peut entraîner une amélioration plus tard, on peut donc autoriser une modification locale du réseau provoquant une augmentation de fonction d'erreur avec une certaine probabilité. Cette probabilité doit tenir compte de l'ampleur de l'augmentation (plus l'augmentation est importante moins la probabilité que celle-ci soit acceptée est grande) et du temps d'apprentissage. En effet, quand le réseau de neurone atteint des résultats acceptables nous devons avoir un paramètre de contrôle qui rendra de moins en moins probable les transformations désavantageuses (c'est le rôle de la température dans le recuit métallurgique).
Nous pouvons définir cette probabilité en nous inspirant de la distribution de Gibbs-Boltzmann, on effectue une transformation qui nous permet de passer de l'état  à l'état
à l'état  et on calcule la variation
et on calcule la variation
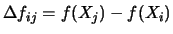 de la fonction
de la fonction  représentant l'erreur en sortie du réseau de neurone, et on accepte la transformation avec la probabilité
représentant l'erreur en sortie du réseau de neurone, et on accepte la transformation avec la probabilité  définie par :
définie par :


 joue ici le rôle de
joue ici le rôle de  que nous avons vu précédemment, nous le désignerons par température.
que nous avons vu précédemment, nous le désignerons par température.
Quand  sera élevé (ce qui sera le cas initialement) un grand nombre de transformations seront acceptées, le réseau de neurones sera instable. A l'inverse quant
sera élevé (ce qui sera le cas initialement) un grand nombre de transformations seront acceptées, le réseau de neurones sera instable. A l'inverse quant  sera proche de
sera proche de  le réseau sera gelé, seules les transformations avantageuses seront acceptées (on espérera alors être proche d'un optimum).
Une transformation désavantageuse sera acceptée si en tirant un nombre aléatoire entre
le réseau sera gelé, seules les transformations avantageuses seront acceptées (on espérera alors être proche d'un optimum).
Une transformation désavantageuse sera acceptée si en tirant un nombre aléatoire entre  et
et  celui-ci se révèle inférieur à
celui-ci se révèle inférieur à  .
.
Mais ou faisons nous intervenir le pas d'apprentissage dans tout ceci, comment celui-ci sera géré ? Reprenons les contraintes que doit avoir le pas : avoir un pas élevé à l'initialisation nous permettra d'accélérer l'apprentissage puis plus la température baissera plus nous baisserons le pas parallèlement afin d'affiner au fur et à mesure le réseau de neurone.
solution initiale X (réseau de neurone généré avec des poids aléatoires)
Xmeilleur <- X
fmin <- f(Xmeilleur) (f étant l'erreur en sortie du reseau)
initialisation de la température t
initialisation du pas à p = 1
Tant que condition 1 faire
(dans cette boucle on essaye les transformations pour une température et
un pas donné)
Tant que condition 2 faire
(à chaque passage dans cette boucle on essaye une transformation
et on détermine si elle est acceptée)
X' <- retropropagation du gradient avec X comme tableau de poids et un pas p
Varf <- f(X') - f(X)
Si Varf < 0 alors (on adopte toute configuration faisant descendre)
X <- X'
Si f(X) < fmin alors (on conserve la meilleure configuration)
fmin <- f(X)
Xmeilleur <- X
Sinon (on ne rejette pas systématiquement une configuration augmentant l'erreur)
on tire a dans [0;1]
Si p <= exp(-Varf/t) alors
X <- X' (acceptation propre au recuit)
Fin si
Fin si
Fin si
Fin tant que
t <- g(t)
p <- h(t)
FIn tant que
retourner Xmeilleur
- La variable que l'on cherche à optimiser est bien entendu le tableau de poids synaptiques du réseau de neurone.
- La température t est initialisée à une valeur variable selon l'expérience.
- La condition 1 est le plus souvent le nombre de changements de température que l'on souhaite effectuer.
- La condition 2 est le nombre de transformations que l'on effectue à une température et à un poids donné.
- Les fonctions
 et
et  sont des suites géométriques décroissantes.
sont des suites géométriques décroissantes.
Nous avons donc mis au point un système de mise à jour du pas en temps réel avec l'apprentissage. Celui-ci nous permet, en plus de converger plus vite vers un optimum, de pouvoir ``affiner'' le réseau de neurone en fin d'apprentissage avec des pas très petits. Cependant cette méthode n'ayant, à notre connaissance, jamais été développée auparavant nous avons eu peu de données et il nous faudra encore de nombreux tests expérimentaux afin d'obtenir une solution qui nous convienne.




suivant: Traitement du signal Création
monter: SOUTENANCE FINALE MARVIN (Modest-encoding
précédent: Le projet
Table des matières
root
2002-06-18
![\includegraphics[]{apprentissage.ps}](img1.png)
![\includegraphics[]{apprentissage.ps}](img1.png)
![\includegraphics[]{recognition.ps}](img2.png)
![\includegraphics[height=2cm]{prim.ps}](img3.png)
![\includegraphics[height=10cm]{emp.ps}](img5.png)
![\includegraphics[]{pmc.ps}](img24.png)
![\includegraphics[height=5cm]{neurone.ps}](img34.png)
![\includegraphics[]{rppmc.ps}](img35.png)
![\includegraphics[]{gradient.ps}](img53.png)






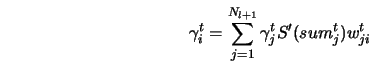
![\includegraphics[]{tdnn.ps}](img74.png)

![\includegraphics[height=5cm]{recuit.ps}](img85.png)
![]() sera élevé (ce qui sera le cas initialement) un grand nombre de transformations seront acceptées, le réseau de neurones sera instable. A l'inverse quant
sera élevé (ce qui sera le cas initialement) un grand nombre de transformations seront acceptées, le réseau de neurones sera instable. A l'inverse quant ![]() sera proche de
sera proche de ![]() le réseau sera gelé, seules les transformations avantageuses seront acceptées (on espérera alors être proche d'un optimum).
Une transformation désavantageuse sera acceptée si en tirant un nombre aléatoire entre
le réseau sera gelé, seules les transformations avantageuses seront acceptées (on espérera alors être proche d'un optimum).
Une transformation désavantageuse sera acceptée si en tirant un nombre aléatoire entre ![]() et
et ![]() celui-ci se révèle inférieur à
celui-ci se révèle inférieur à ![]() .
.