



suivant: Cryptographie
monter: SOUTENANCE FINALE MARVIN (Modest-encoding
précédent: Structures d'apprentissage & Réseaux
Table des matières
Sous-sections
Dans le projet MARVIN, une des composantes principale mais aussi une des grande difficulté est la création de l'empreinte vocale. En effet, nous devons concevoir celle-ci afin qu'elle soit trés caractéristique d'un individu (deux individus différents auront une empreinte distincte) tout en restant à peu près la même pour le même locuteur.
Cette partie présentera les différents développements et recherches qui ont été effectués autour de cet objectif. Le principe général est assez simple : après avoir recupéré le signal vocal et s'être placé sur une voyelle, nous transformons le signal en représentation fréquentielle de façon à récupérer une empreinte bien spécifique à l'utilisateur. Pour cela, nous utilisons la MFCC (Mel Frequency Cepstral Coefficients) qui elle même est l'application, comme nous le verrons par la suite de la FFT (Fast Fourier Transform) et de la DCT (Discret Cosinus Transform).
Schéma général de fonctionnement
Signal échantillonné
Energie du signal
Echantillonage du signal au point de plus haute énergie
MFCC sur cette partie du signal (plan 3D)
MFCC sur cette partie du signal (plan 2D)
Empreinte vocale (moyenne)
La MFCC est la dernière amélioration que nous avons effectué dans le fonctionnement de MARVIN. La méthode précedente, une application directe de la FFT sur une certaine partie du signal, ne nous donnait pas de résultats assez bon et le taux d'erreur en reconnaissance était trop important, ceci rendant son utilisation caduque.
La MFCC (Mel Frequency Cepstral Coefficients) est une extraction de caractéristique du signal développée autour de la FFT et de la DCT, ceci sur une échelle de Mel. Nous avons découvert ce principe (qui finalement paraît être le plus utilisé en identification du locuteur) grâce à un article d'un laboratoire de recherche de Jussieu : le LISIF.
La MFCC se décompose en phases :
- Phase 1 : Découper le signal en plusieurs fenêtres qui se recoupent entre elles.
Par exemple si nous découpons un signal en X fenêtres de 256, avec un recoupement de 100,
alors, la première fenêtre sera 0-255, la seconde 155-411, etc ...
Nous appliquerons la MFCC à chaque fenêtre.
- Phase 2 : Afin de diminuer la distortion spectrale nous appliquons une fenêtre de Hamming au signal :
Par la suite nous multiplions cette fonction par le signal à transformer, nous minimisons ainsi la distortion spectrale créée
par le recoupement.
- Phase 3 : Appliquer ensuite la FFT à la fenêtre pour en ressortir la magnitude, on obtient donc le spectre.
- Phase 4 : On passe à l'échelle de Mel. En effet, après des études sur l'ouie humaine, il a été montré
que l'homme se base sur une échelle fréquencielle spécifique.
La formule de transfert est simple :
Pour simuler l'oreille humaine, il faut passer par un Banc Filtre,
un filtre pour chaque fréquence que l'on cherche.
Ces filtres ont une réponse de bande passante triangulaire.
Pour connaitre l'intervalle entre chaque filtre, on utilise
une constante: Mel-Frequency interval.
Nous utilisons 20 filtres.
- Phase 5 : Pour finir, nous travaillons avec le Cepstre, nous convertissons le spectre logarithmique de Mel en temps au moyen de la DCT (Discret Cosinus Transform). La formule de cette transformation est simple :
N est la taille du signal.
Ainsi, nous réduisons le nombre de données caractérisant le signal et nous en ressortons 13 (dans notre cas) coefficients cepstraux par fenêtre ( 6 dans notre cas).
En général, il est conseillé de travailler sur ces coefficients cepstraux en
prenant en compte toutes les sous fenêtres.
Dans notre cas, vu que l'on veut retrouver juste une empreinte caractéristique,
nous faisons la moyenne des sous empreintes de la portion de signal sur laquelle nous travaillons, ce qui nous donne au final
une empreinte trés caractéristique.
L'implémentation de la MFCC nous posa de nombreux problèmes. En effet, la théorie trouvée sur internet ne nous permettait pas de pousser très loin nos recherches (en particulier le banc de filtres). Cependant les tâtonnements et les résultats de Matlab nous ont permis d'arriver peu à peu à une solution satisfaisante.
![\includegraphics[height=12cm]{mfccmarvin.ps}](img109.png)
MFCC sur le mot 'marvin'
Empreinte vocale (sujet 1)
Empreinte vocale 2 (sujet 1)
Empreinte vocale 3 (sujet 1)
Empreinte vocale 3 (sujet 2)
Notre projet n'a pas toujours eu le même principe. Avant de commencer MARVIN, nous n'avions aucune connaissances en traitement du signal. Nous sommes donc passé par énormement d'étapes et de tâtonnements.
Nous nous sommes donc intéressé a plusieurs traitements :
- L'acquisition
- La FFT
- Le Cepstre
- Hamming
- Le Spectrographe
- Le spline cubique
- La DCT
- La MFCC
- Le LPC
Toutes ces opérations ont été recodées (à part le LPC), mais pas toutes utilisées (Spectrogramme, Spline, LPC). Nous allons dans la suite de cette partie présenter le cheminement de nos recherches.
L'acquisition est vraiment une partie dont l'intérêt mathématique est nul
et ce n'est que du code pur, donc rien d'intérressant. Mais en voici tout de même le fonctionnement.
Dans cette partie, nous devions faire une procédure qui nous permettait de
récupérer par le microphone un tableau Amplitude / Secondes : A(dB) / t(s).
La carte son renvoie dans son fichier "device" associé (/dev/audio ou /dev/dsp),
des octets correspondant aux dB rentrés dans le microphone.
Le procédé est simple :
- Tout d'abord, il y a la voix qui crée des ondes. Celles-ci percutent le micro qui renvoie à la carte son la valeur de la dépression / pression. La carte son convertit la pression (en Pascal) en décibels par rapport à une pression de référence (le silence).
- Ensuite le CAN (convertisseur analogique/numérique)
renvoie cette valeur après étalonnage au /dev/dsp (ou /dev/audio).
- On récupère cette valeur qui est l'amplitude et on la range dans un buffer. Ainsi nous obtenons un buffer comprenant chaque échantillon.
Comment récupérer les octets ressortant de la carte son ?
Nous avions tout d'abord pensé utiliser une librairie de son mais aucune ne nous paraissait utilisable soit par le manque de la fonction d'enregistrement du son soit par la lourdeur imposée. Ensuite, en collaboration avec un autre groupe, nous avions trouvé un programme C qui faisait l'enregistrement sans lib extraordinaire. Nous voulions en extraire ses fonctions d'enregistrement. Puis à force de chercher des informations sur les devices, nous avons vite compris que beaucoup de fonctions existaient déjà. Ainsi open (de /dev/dsp) nous permet de faire une copie bit à bit de ce qui ressort du device. Tout cela marche grace à la fonction IOCTL.
Au final, on ressort un son de fréquence 11025Hz.
La transformée de Fourier s'applique aussi bien sur les signaux continus (périodiques ou pas) que sur les signaux discrets. C'est ce dernier cas qui nous intérresse dans la mesure où lors de l'acquisition, les données que l'on enregistre sont des ensembles de valeurs à des instants périodiques dans le temps. Ce sont des valeurs représentant des signaux échantillonnés (quelconques). Nous allons donc utiliser la transformée de Fourier appliquée à ces types de signaux.
Soit un signal périodique 
On suppose que le signal est périodique de période T (qui est supérieure à l'interval sur lequel on l'a coupé) et que l'on a la fonction qui permet d'obtenir cette représentation, on l'appelle  .
Le développement en séries de Fourrier d'une fonction périodique est l'approximation de cette fonction par une série d'autres fonctions sinusoidales. Par exemple si on a deux fonctions continues
.
Le développement en séries de Fourrier d'une fonction périodique est l'approximation de cette fonction par une série d'autres fonctions sinusoidales. Par exemple si on a deux fonctions continues 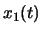 et
et  sur un intervalle [t1 ; t2] et on cherche à approximer
sur un intervalle [t1 ; t2] et on cherche à approximer 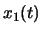 par
par  . Il s'agit de trouver un scalaire
. Il s'agit de trouver un scalaire 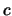 tel que :
tel que :
Pour la minimisation de l'erreur quadratique, on a :
On constate que 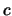 est minimum pour
est minimum pour
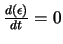 c'est à dire
c'est à dire
Exemple, on a un signal rectangulaire de période  et d'amplitude 1. On a
:
et d'amplitude 1. On a
:
 d'où
d'où
 .
On utilise le même procédé si on veut approximer une fonction continue
.
On utilise le même procédé si on veut approximer une fonction continue  par une famille de fonctions continues
par une famille de fonctions continues  et qui possède la propriété:
et qui possède la propriété:
on a :
ainsi
Par exemple, si on reprend l'exemple précédent,
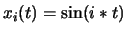 , d'où
, d'où
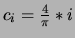 si i impair ou
si i impair ou  si i pair.
si i pair.
pour 
Cette première approche vous donne une idée globale de l'utilité des coefficients 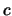 pour l'approximation d'une fonction.
Revenons au signal périodique
pour l'approximation d'une fonction.
Revenons au signal périodique  de période T.
Une onde (représentation d'une période de xT) peut être décomposée en une superposition d'ondes sinusoïdales. Celles-ci sont liées de façon harmonique c'est à dire que leur fréquence sont des harmoniques (des multiples) d'une fondamentale (fréquence minimale ).
de période T.
Une onde (représentation d'une période de xT) peut être décomposée en une superposition d'ondes sinusoïdales. Celles-ci sont liées de façon harmonique c'est à dire que leur fréquence sont des harmoniques (des multiples) d'une fondamentale (fréquence minimale ).
- la première harmonique (fondamentale) a une fréquence

- la deuxième

- la troisième

- la quatrième
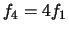
- ...
- ...
En appliquant la série de Fourrier sur  , on obtient :
, on obtient :
avec
 composante continue qui représente la moyenne de
composante continue qui représente la moyenne de  .
.
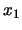 harmonique 1,
harmonique 1,  harmonique 2,
harmonique 2, 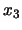 harmonique 3,...,
harmonique 3,..., 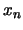 harmonique n
harmonique n
On a alors :
On admet qu'une onde périodique est une superposition d'ondes sinusoïdales harmoniquement liées.
Par la méthode de Fourrier, on peut passer de l'analyse temporelle d'un signal à son analyse fréquentielle.
Posons D la valeur de crête à crête d'une onde périodique :
 .
.
Le spectre du signal  va nous donner un graphique où sera représenté en abcisses la fréquence (correspondant à la fréquence des différentes harmoniques de xT) et en ordonnées la valeur de crête associée (pour chaque harmonique).
Normalement, le spectre d'un signal varie d'un signal périodique à un autre.
Dans le cadre de la décomposition du signal sonore, on va pouvoir se servir des valeurs de crêtes des différentes harmoniques pour distinguer chaque enregistrement.
va nous donner un graphique où sera représenté en abcisses la fréquence (correspondant à la fréquence des différentes harmoniques de xT) et en ordonnées la valeur de crête associée (pour chaque harmonique).
Normalement, le spectre d'un signal varie d'un signal périodique à un autre.
Dans le cadre de la décomposition du signal sonore, on va pouvoir se servir des valeurs de crêtes des différentes harmoniques pour distinguer chaque enregistrement.
Revenons à un cas plus général : supposons que l'ensemble des fonctions  soient constituées
soient constituées
avec
 on en déduit :
on en déduit :
pour  et
et
avec
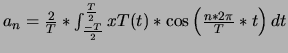


On obtient une décomposition de xT(t) en séries de Fourier
avec
 pour n > 0
pour n > 0
 pour n < 0
pour n < 0

d'où
 est appelée coefficient de Fourrier.
est appelée coefficient de Fourrier.
La suite des coefficients complexes  constitue le spectre (de raies) du signal périodique xT(t). Par analogie avec le cas particulier de l'onde,
constitue le spectre (de raies) du signal périodique xT(t). Par analogie avec le cas particulier de l'onde,  représente la valeur de crête de l'harmonique n de l'onde.
On suppose à présent qu'on a un signal
représente la valeur de crête de l'harmonique n de l'onde.
On suppose à présent qu'on a un signal  non périodique (dont on connaît l'équation) qui est pris sur un temps T.
non périodique (dont on connaît l'équation) qui est pris sur un temps T.
 étant non périodique, on peut le considérer comme une fonction périodique de période T avec T qui tend vers l'infini.
Posons
étant non périodique, on peut le considérer comme une fonction périodique de période T avec T qui tend vers l'infini.
Posons
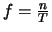 ;
f est comparable à une fréquence et correspond par analogie au premier cas à la fréquence de l'harmonique n. Le spectre de
;
f est comparable à une fréquence et correspond par analogie au premier cas à la fréquence de l'harmonique n. Le spectre de  serait continu si celui-ci n'était pas identiquement nul.
Appelons
serait continu si celui-ci n'était pas identiquement nul.
Appelons 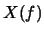 la transformée de Fourrier de
la transformée de Fourrier de  (spectre de
(spectre de  ).
).
les conditions pour qu'on puisse appliquer la transformée de Fourrier sur une fonction  non périodique sont :
non périodique sont :
 doit être une fonction bornée.
doit être une fonction bornée.
-
 a une valeur finie.
a une valeur finie.
- la discontinuité de
 ainsi que les maximums et minimums est en valeur finie.
ainsi que les maximums et minimums est en valeur finie.
Signal discret
On suppose que le signal  que l'on doit étudier n'est pas connu, c'est-à-dire qu'il n'existe pas de fonction qui permette de représenter
que l'on doit étudier n'est pas connu, c'est-à-dire qu'il n'existe pas de fonction qui permette de représenter  en fonction du temps,(c'est un signal discontinu).
Cette hypothèse semble la plus probable étant donné que chaque enregistrement de voie semble unique. C'est sous cette forme que se presentera le signal par la suite.
Le signal
en fonction du temps,(c'est un signal discontinu).
Cette hypothèse semble la plus probable étant donné que chaque enregistrement de voie semble unique. C'est sous cette forme que se presentera le signal par la suite.
Le signal  est donc constitué d'un ensemble de signaux
est donc constitué d'un ensemble de signaux  qui sont définis que pour des instants appartenant à un ensemble dénombrable.
t= {t1,t2,...,tn} et on note
qui sont définis que pour des instants appartenant à un ensemble dénombrable.
t= {t1,t2,...,tn} et on note  .
{
.
{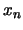 } est appelé signal discret.
} est appelé signal discret.
Supposons qu'il y ait une relation entre les éléments de la suite {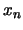 };
};
La transformation de Fourier du signal {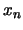 } est :
} est :
X(f) est un signal périodique de periode 1.
Cette transformation n'existe que si les signaux sont absolument sommables :
on obtient alors :
|X(f)| le spectre fréquentiel d'amplitude de {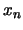 } et qui est une fonction paire.
} et qui est une fonction paire.
 le spectre fréquentiel de phase de {
le spectre fréquentiel de phase de {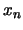 } et qui est une fonction impaire
} et qui est une fonction impaire
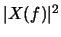 le spectre d'énergie de {
le spectre d'énergie de {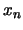 }.
}.
Maintenant, il existe le problème du calcul de f et le cas où le nombre de 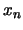 est infini.
Pour le résoudre:
on pose
est infini.
Pour le résoudre:
on pose
 avec N points entre 0 et 1.
avec N points entre 0 et 1.
 h= 0,1,2,3,...,N
h= 0,1,2,3,...,N
or
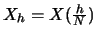
posons a nouveau
 on a :
on a :
si  s'annule à partir de n = N
s'annule à partir de n = N
 est appelée transformée de Fourrier discrète (TFD), d'ordre N.
on peut représenter la TFD sous forme matricielle en mettant :
est appelée transformée de Fourrier discrète (TFD), d'ordre N.
on peut représenter la TFD sous forme matricielle en mettant :
-
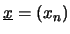 vecteur colonne de dimension N
vecteur colonne de dimension N
-
 " " "
" " "
-
![$W = [W^{(n*k)}]$](img189.png) matrice
matrice  symétrique.
symétrique.
on a donc :

ceci constitue les premieres recherches qui nous ont permis de coder la transformee de Fourierpar la suite en utilisant la TFD basee sur l'algorithme de Cooley et Turkey.
La TFD permet de passer de la représentation temporelle d'un signal à sa représentation fréquentielle. Elle est définie de la manière suivante:
avec :
 le nombre total d'échantillons.
le nombre total d'échantillons.
 l'amplitude de l'échantillon à la position
l'amplitude de l'échantillon à la position  .
.
On fait varier  de 1 jusqu'au nombre total de valeurs que l'on désire.
de 1 jusqu'au nombre total de valeurs que l'on désire.
Supposons maintenant que l'on dispose d'un enregistrement de N échantillons
et que l'on cherche à appliquer la TFD sur ce signal.
En se servant d'un algorithme qui appliquerait la formule, le calcul de chaque
valeur de  nécessiterait
nécessiterait  additions et
additions et  multiplications complexes. Si on
veut
multiplications complexes. Si on
veut  valeurs de
valeurs de  , l'algorithme nécessiterait donc
, l'algorithme nécessiterait donc  additions et
additions et  multiplications complexes. Étant donné que le nombre d'échantillons que l'on a
pour chaque enregistrement est très élevé (de même pour le nombre de valeurs
désirées), l'application de cet algorithme nous prendrait beaucoup de temps et ralentirait le programme.
Ce qui nous a conduit à appliquer la Transformée de Fourier Rapide (qui est
moins coûteux en temps).
En effet, nous avons tenté de coder Fourier sans la FFT (une Fourier lente en somme) mais la recherche exhaustive et les opérations demandent réellement trop de temps à la machine.
La FFT s'applique sur un signal dont le nombre d'échantillons est une puissance de 2. L'algorithme de la FFT a été mise au point en 1965 par Cooley et Tuckey.
La FFT est une version rapide de la TFD.
Racines complexes de l'unité:
On définit une n ième racine complexe de l'unité un nombre complexe
multiplications complexes. Étant donné que le nombre d'échantillons que l'on a
pour chaque enregistrement est très élevé (de même pour le nombre de valeurs
désirées), l'application de cet algorithme nous prendrait beaucoup de temps et ralentirait le programme.
Ce qui nous a conduit à appliquer la Transformée de Fourier Rapide (qui est
moins coûteux en temps).
En effet, nous avons tenté de coder Fourier sans la FFT (une Fourier lente en somme) mais la recherche exhaustive et les opérations demandent réellement trop de temps à la machine.
La FFT s'applique sur un signal dont le nombre d'échantillons est une puissance de 2. L'algorithme de la FFT a été mise au point en 1965 par Cooley et Tuckey.
La FFT est une version rapide de la TFD.
Racines complexes de l'unité:
On définit une n ième racine complexe de l'unité un nombre complexe  tel que :
tel que :
Il y a  racines n ième complexe de l'unité. Elles valent :
racines n ième complexe de l'unité. Elles valent :
pour k = 0, 1, ..., n-1
En utilisant la définition de l'exponentielle
On constate que les n racines complexes de l'unité sont espacées de façon régulière autour d'un cercle de rayon unitaire centré à l'origine du plan complexe. La valeur
est appelée la racine n ième principale de l'unité. On voit que :
ce qui entraîne :
De même,
Remarque :
* Lemme de l'annulation :
 , et
, et  ,
,
* pour
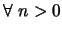 , avec
, avec  pair :
pair :
* Lemme de la bipartition :
Si 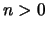 est pair, les carrés des n racines nièmes de l'unité sont les
est pair, les carrés des n racines nièmes de l'unité sont les  racines
racines 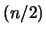 iemes de l'unité.
iemes de l'unité.
Démonstration
D'après le lemme de l'annulation, on a :
pour tout entier positif k.
On remarque que l'on élève au carré toutes les racines  ièmes de l'unité, chaque racine
ièmes de l'unité, chaque racine 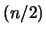 ième de l'unité est obtenue exactement deux fois, puisque
ième de l'unité est obtenue exactement deux fois, puisque
donc  et
et  ont le même carré.
ont le même carré.
Ce lemme est important pour l'approche "diviser pour régner" dont nous nous servirons dans le calcul récursif de la FFT.
* Lemme de la sommation :
 entier
entier  , et
, et  entier positif
entier positif  non divisible par
non divisible par  ,
,
Principe de la Transformée de Fourier Rapide :
La FFT tire parti des propriétés particulières des racines complexes de
l'unité, elle permet de calculer la TFD en  opérations. Elle fait appel à
une stratégie "diviser pour régner", en utilisant séparément les coefficients
d'indice pairs et impairs de A(j) qui représente une série de n échantillons; pour
définir les deux nouvelles séries A[0] et A[1] de longueur n/2 :
opérations. Elle fait appel à
une stratégie "diviser pour régner", en utilisant séparément les coefficients
d'indice pairs et impairs de A(j) qui représente une série de n échantillons; pour
définir les deux nouvelles séries A[0] et A[1] de longueur n/2 :
A[0] = { a(0) ; a(2) ; a(4) ; a(6) ; ... ; a(n-2) }
A[1] = { a(1) ; a(3) ; a(5) ; a(7) ; ... ; a(n-1) }
On constate que A[0] contient tous les coefficients d'indice pair de A (la
représentation binaire de l'indice se termine par 0), et que A[1] contient
tous les coefficients d'indice impair (la représentation binaire de l'indice
se termine par 1). On a :
![$A(j) = A[0] + A[1]$](img222.png)
Problème qui consiste à évaluer A(j) en  ,
,  ,
, 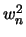 , ...,
, ...,  se
ramène a évaluer les deux séries A[0] et A[1] de longueur
se
ramène a évaluer les deux séries A[0] et A[1] de longueur  aux points
aux points
 ,
,  ,
,  , ...,
, ..., 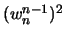
D'après les remarques faites ci-dessus, cette liste de valeurs est composée
seulement de  racines
racines  ièmes de l'unité, chaque racine apparaissant
exactement 2 fois. Ainsi les séries A[0] et A[1] de longueur
ièmes de l'unité, chaque racine apparaissant
exactement 2 fois. Ainsi les séries A[0] et A[1] de longueur  sont utilisées
récursivement pour les
sont utilisées
récursivement pour les  racines
racines  ièmes de l'unité. Ces sous problèmes
ont exactement la même forme que le problème initial, mais sont moins grands de
moitié.
ièmes de l'unité. Ces sous problèmes
ont exactement la même forme que le problème initial, mais sont moins grands de
moitié.
Nous avons réduit un calcul de la TFD à  éléments en 2 calcul de TFD à
éléments en 2 calcul de TFD à  éléments. Cette décomposition est a l'origine du principe algorithmique décrit
ci-dessous :
éléments. Cette décomposition est a l'origine du principe algorithmique décrit
ci-dessous :
FFT Recc(A)
/* A est un tableau qui représente les échantillons d'une acquisition vocale */
1 
 longueur(A)
/* n est une puissance de 2 */
longueur(A)
/* n est une puissance de 2 */
2 si  = 1
= 1
3 alors retourne A
4 


5 
 1
1
6 A[0]  { a(0) ; a(2) ; a(4) ; ... ; a(n-2) } /* tableau des valeurs d'indice pair de A */
{ a(0) ; a(2) ; a(4) ; ... ; a(n-2) } /* tableau des valeurs d'indice pair de A */
7 A[1]  { a(1) ; a(3) ; a(5) ; ... ; a(n-1) } /* tableau des valeurs d'indice impair de A */
{ a(1) ; a(3) ; a(5) ; ... ; a(n-1) } /* tableau des valeurs d'indice impair de A */
8 y[0]  FFT Recc(A[0])
FFT Recc(A[0])
9 y[1]  FFT Recc(A[1])
FFT Recc(A[1])
10 pour 
 0 à
0 à  - 1 faire
- 1 faire
11 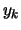

![$y_k[0] + w * y_k[1]$](img235.png)
12 

![$y_k[0] - w * y_k[1]$](img237.png)
13 


14 retourne 
Fonctionnement de la fonction FFT Recc :
La TFD d'un élément est l'élément lui même, car dans ce cas :
Les lignes 6 et 7 définissent les séries A[0] et A[1]. Les lignes 4, 5, et 13
garantissent que  est bien mis a jour de sorte qu'a chaque exécution des
lignes 11 et 12,
est bien mis a jour de sorte qu'a chaque exécution des
lignes 11 et 12,  . Les lignes 8 et 9 calculent récursivement les TFD
en
. Les lignes 8 et 9 calculent récursivement les TFD
en  , en effectuant pour k = 0, 1, ..., n/2-1, les affectations :
, en effectuant pour k = 0, 1, ..., n/2-1, les affectations :
ou, puisque

Les lignes 11 et 12 combinent les résultats des calculs récursifs de TFD en  pour
pour  ,
,  , ...,
, ...,  , la ligne 11 génère :
, la ligne 11 génère :
La ligne 12 donne :
D'où la série  retourne par FFT Recc est la transformée discrète de la série
retourne par FFT Recc est la transformée discrète de la série  .
C'est ce principe que nous avons utilise pour appliquer la transformée de
Fourier sur un ensemble de valeurs donnés par un enregistrement.
Après avoir étudié pas mal de codes ...nous nous sommes lancé nous même dans notre propre implémentation (une dérive de ButterFly).
Nous nous somme basé sur un tableau de complexes dont le type est DOUBLE. La fonction en elle même prend en paramètre le tableau de complexe en entrée et le tableau de sortie ainsi que la taille
de la fenêtre
le nombre de bits utilisé pour la FFT (le coefficient de la puissance de 2) est calculé en travaillant directement
sur la mémoire (ou se trouve le 1 des octets du nombre )
le oméga, l'angle initialisé est normalement à
.
C'est ce principe que nous avons utilise pour appliquer la transformée de
Fourier sur un ensemble de valeurs donnés par un enregistrement.
Après avoir étudié pas mal de codes ...nous nous sommes lancé nous même dans notre propre implémentation (une dérive de ButterFly).
Nous nous somme basé sur un tableau de complexes dont le type est DOUBLE. La fonction en elle même prend en paramètre le tableau de complexe en entrée et le tableau de sortie ainsi que la taille
de la fenêtre
le nombre de bits utilisé pour la FFT (le coefficient de la puissance de 2) est calculé en travaillant directement
sur la mémoire (ou se trouve le 1 des octets du nombre )
le oméga, l'angle initialisé est normalement à  mais dans notre cas, on prendra
mais dans notre cas, on prendra  pour avoir
les même résultats que Matlab.
Ensuite, après les initialisations, on vérifie que le nombre d'échantillons sur lesquels on travaille est bien une
puissance de 2.
Après, on copie les données sur le tableau de sortie et on fait l'inversion des bits en même temps, cela en travaillant toujours
sur les octets.
Ensuite on parcourt le tableau toute les puissances de deux ( échantillons 2, 4, 8 ...) et à chaque fois, on parcours la suite du tableau.
On prends un petit delta de l'angle (oméga par rapport ou l'on est) et on applique les équations de Fourier.
On modifie le tableau en conséquence à chaque fois.
Ensuite on normalise.
Voilà.
On a fait les quelques optimisations découvertes dans les autres codes. Spécialement le fait de travailler bit à bit et non sur les doubles
directement.
Le cepstre est utilisé pour l'analyse spectrale homomorphique, et il permet aussi d'extraire la fréquence fondamentale d'un signal de la parole et de déterminer la fréquence des formants.
On distingue le cepstre complexe et le cepstre réel (qui est celui dont nous nous sommes servis).
En général, particulièrement dans le signal de parole, le signal reçu
pour avoir
les même résultats que Matlab.
Ensuite, après les initialisations, on vérifie que le nombre d'échantillons sur lesquels on travaille est bien une
puissance de 2.
Après, on copie les données sur le tableau de sortie et on fait l'inversion des bits en même temps, cela en travaillant toujours
sur les octets.
Ensuite on parcourt le tableau toute les puissances de deux ( échantillons 2, 4, 8 ...) et à chaque fois, on parcours la suite du tableau.
On prends un petit delta de l'angle (oméga par rapport ou l'on est) et on applique les équations de Fourier.
On modifie le tableau en conséquence à chaque fois.
Ensuite on normalise.
Voilà.
On a fait les quelques optimisations découvertes dans les autres codes. Spécialement le fait de travailler bit à bit et non sur les doubles
directement.
Le cepstre est utilisé pour l'analyse spectrale homomorphique, et il permet aussi d'extraire la fréquence fondamentale d'un signal de la parole et de déterminer la fréquence des formants.
On distingue le cepstre complexe et le cepstre réel (qui est celui dont nous nous sommes servis).
En général, particulièrement dans le signal de parole, le signal reçu  résulte de la convolution (produit) d'une excitation
résulte de la convolution (produit) d'une excitation  (le signal de la source) et d'une réponse impulsionnelle
(le signal de la source) et d'une réponse impulsionnelle  (le bruit) :
(le bruit) :
Par une opération appelée déconvolution l'analyse homomorphique permet dans certain cas de séparer les signaux  et
et  .
Le principe de la méthode est de calculer le logarithme de la transformée en
.
Le principe de la méthode est de calculer le logarithme de la transformée en  du signal (que l'on appelle
du signal (que l'on appelle  ) dont on déterminera par la suite l'original. Ainsi, le signal
) dont on déterminera par la suite l'original. Ainsi, le signal  obtenu de
obtenu de  par une opération non linéaire est appelé cepstre complexe associé au signal
par une opération non linéaire est appelé cepstre complexe associé au signal  . On a :
. On a :
L'espace de représentation du cepstre (appelé espace quéfrentiel) est homogène au temps.
On peut parfois arriver à isoler les signaux  et
et  par filtrage temporel. Pour cela, on applique l'opération inverse sur
par filtrage temporel. Pour cela, on applique l'opération inverse sur  et
et  afin d'obtenir
afin d'obtenir  et
et  .
Si on dispose d'un signal minimum phase, alors on peut calculer son cepstre a partir du module de la transformée de Fourier. Si
.
Si on dispose d'un signal minimum phase, alors on peut calculer son cepstre a partir du module de la transformée de Fourier. Si  est un signal réel alors
est un signal réel alors  sera aussi réel.
Le cepstre réel est la transformation que nous avons employé pour avoir la fréquence fondamentale d'un enregistrement de voix et la fréquence des formants (qui la constituent).
Pour calculer le cepstre réel on applique la formule la plus classique : Elle se sert de la transformée de Fourier à court terme, basée sur l'application de 2 TFD(transformée de Fourier discrète).
Au départ, on suppose qu'on dispose d'un enregistrement de voix échantillonné f(n) qui est la convolution du signal de la source par le filtre correspondant au conduit :
sera aussi réel.
Le cepstre réel est la transformation que nous avons employé pour avoir la fréquence fondamentale d'un enregistrement de voix et la fréquence des formants (qui la constituent).
Pour calculer le cepstre réel on applique la formule la plus classique : Elle se sert de la transformée de Fourier à court terme, basée sur l'application de 2 TFD(transformée de Fourier discrète).
Au départ, on suppose qu'on dispose d'un enregistrement de voix échantillonné f(n) qui est la convolution du signal de la source par le filtre correspondant au conduit :
 . On applique une première transformée discrète sur le signal et on obtient le signal F(n). Ensuite, on calcule son module, on met la partie imaginaire du signal à 0 et on se sert du log du signal pour séparer les 2 composants :
. On applique une première transformée discrète sur le signal et on obtient le signal F(n). Ensuite, on calcule son module, on met la partie imaginaire du signal à 0 et on se sert du log du signal pour séparer les 2 composants :
Enfin, on applique une FFT inverse sur ce signal. Le cepstre réel correspond à la partie réelle de ce qu'on a en sortie.
- Application à la détermination des formants :
Dans un enregistrement vocal, les formants sont des traits caractéristiques des voyelles et de certaines consonnes. Sur la représentation spectrale d'un signal, les formants correspondent à des niveaux d'énergie élevé. Ainsi , on peut facilement détecter la fréquence des trois premiers formants sur un signal.
Pour les hommes, la fréquence de ces 3 premiers formants est inférieure à 5000 Hz.
On pourra aussi se servir du cepstre pour lisser le spectre afin d'observer ces formants.
- Application à la détermination de la fréquence fondamentale :
On se sert du cepstre pour lisser un signal comme il a été dit précédemment . Les premiers coefficients cepstraux permettent de lisser la représentation spectrale équivalente car ils contiennent les informations importantes relatives au spectre . Ces coefficients deviennent négligeables à partir d'une certaines fréquence N.
Le cepstre est une représentation de l'information spectrale pour laquelle une opération de filtrage linéaire se traduit par une modification additive (c'est le principe du traitement de signal homomorphique), utile pour les enregistrement téléphoniques.
Le cepstre fournit une méthode pour réduire la quantité d'information dans la mesure ou en conservant les premiers coefficients cepstraux, on peut lisser la représentation spectrale d'un signal afin de conserver l'enveloppe spectrale caractéristique du signal de la parole.
Les coefficients cepstraux reflètent les variations du spectre à court terme du signal de parole. Les ordres de grandeur des fréquences fondamentales sont de 120 Hz pour les hommes 250 Hz pour les femmes et 450 Hz pour les enfants.
A partir d'un nombre de points N du cepstre, le spectre obtenu quand on applique une FFT inverse sur le cepstre donne le même signal qu'en conservant tous les points du cepstre. Au delà de N, le spectre présente des pics périodiques qui sont des harmoniques de la fréquence fondamentale.
Les coefficients cepstraux ne présentent pas des variations intra-locuteurs de même ampleur. La variance des coefficients cepstraux décroît avec leur ordre.
En voici le principe de fonctionnement.
Le principe de l'amplification est simple.
On crée le signal de Hamming, et on le multiplie
a celui que l'on veut amplifier.
L'intérêt est d'effacer progressivement le début et la
fin du signal tout en amplifiant la partie principale.
Pour créer ce signal de Hamming, on utilise cette formule :

où
 est le signal de Hamming,
est le signal de Hamming,
 le nombre d'échantillons
le nombre d'échantillons
 l'échantillon a calculer
l'échantillon a calculer
 et
et  sont deux coefficients, tels que
sont deux coefficients, tels que  .
Dans notre cas on utilisera :
.
Dans notre cas on utilisera :
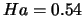 et
et 
Dans un but expérimental, nous avons dû coder
le spectre du signal, une FFT sur tout le signal
qui nous permet de voir l'évolution des fréquences
dans le temps du signal. Cette "image" de la voix
sera entre autre utilisée pour l'aspect graphique
du programme.
L'aspect code n'est toujours qu'une réutilisation
des outils précédemment codés. Ainsi le spectre
ne fut pas très compliqué à coder. Pour afficher
ce spectre, on a utilisé la Xlib.
Une librairie très simple qui affiche tout simplement
un point sur un framebuffer ou l'on veut.
L'outil n'est pas très puissant mais nettement
suffisant pour l'affichage de Spectre.
Décrivons brièvement le fonctionnement :
Nous faisons une FFT de 256 sur les 256 premiers échantillons.
On refait une FFT de 256 sur 256 échantillons mais à partir du
128ème échantillons, etc...
Ainsi, sur 512 échantillons, nous aurons fait 3 FFT,
une de 1 à 256, une de 128 à 384, puis de 256 à 512.
C'est ce que l'on appelle des fenêtres de recouvrement.
L'affichage ce passe alors ainsi :
La couleur (bleu en l'occurrence) peut prendre 256 valeurs.
Nous avons un tableau de
![$256 * [la\ taille\ du\ signal / 128]$](img271.png) Ainsi, nous avons au fur à mesure du signal une FFT
qui sera représentée ainsi :
Ainsi, nous avons au fur à mesure du signal une FFT
qui sera représentée ainsi :
- Verticalement la FFT : 0 pour une amplitude nulle, jusqu'à
256. Ces valeurs seront aussi celles des couleurs des pixels.
- Horizontalement : sa position dans le temps.
Voici le spectre d'un signal :
L'intensité de chaque pixel montre l'amplitude pour la fréquence
associée. On remarque bien la présence des différents mots prononcés.
Ainsi, le spectre représente précisément un w
Après avoir fait la FFT sur le WAV, nous avons pour intention d'en
ressortir l'ensemble caractéristique.
Pour pouvoir rentrer notre partie du signal dans le
réseau de neurones, celui-ci devra être "lisser". Cela veut dire que,
par exemple, si l'on a 200 points mais que le signal final doit faire
20'000 points, on ne va pas simplement compléter les "trous" par des
droites mais par des courbes cubiques de manière à ce que tout le signal
ne forme plus qu'une grande courbe passant par tous ces points. C'est le
principe du spline cubique.
Première approche :
Au début, nous avions l'intention de trouver un polynôme de degré n-1
(ou n est le nombre de points) qui passerait par tous ces points.
Théoriquement, c'est très simple, un simple système d'équation a résoudre,
et trouver le polynôme de plus bas degré et de tracer le plus court.
Le problème, c'est qu'après avoir codé la résolution de l'équation
matricielle obtenue ainsi que le test de degré le plus bas et de tracer
le plus court, l'algorithme se montra terriblement lent. Pour résoudre
ce problème, nous avons travaillé sur une optimisation grâce aux
professeurs de mathématique. En vain, l'algorithme se montrait bien trop
lent (plusieurs minutes en fonction du nombre de points).
Deuxième solution, plus dure mais plus efficace :
Après s'être renseigné sur Internet, nous avons trouver un TIPE que était
dédier aux splines. Dernière chance, comprendre ce charabia mathématique
et tous traduire en algorithme efficace. Pour simplifier l'aspect théorique
du spline cubique, voici une explication courte, simple mais complète.
Nous avons 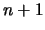 points, on veut une courbe lisse qui passe par ces
points, on veut une courbe lisse qui passe par ces 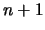 points. Pour ça, nous allons chercher un polynôme cubique qui passe par
chaque couple de points définissant les
points. Pour ça, nous allons chercher un polynôme cubique qui passe par
chaque couple de points définissant les  intervalles.
intervalles.
Les dérivés premières et secondes doivent être continues (pour cela, il
suffit de calculer les pentes). Ensuite, pour choisir le polynômes à prendre
il faut sélectionner celui dont la dérivée est la même que le polynôme précédent
au point d'intersection.
Finalement, grâce à cette technique, le spline marche et nous avons une
jolie courbe qui passe par tous nos points...




suivant: Cryptographie
monter: SOUTENANCE FINALE MARVIN (Modest-encoding
précédent: Structures d'apprentissage & Réseaux
Table des matières
root
2002-06-18
![\includegraphics[]{paol.ps}](img98.png)
![\includegraphics[]{paol.ps}](img98.png)
![\includegraphics[]{wav.ps}](img99.png)
![\includegraphics[]{energie.ps}](img100.png)
![\includegraphics[]{wavenergie.ps}](img101.png)
![\includegraphics[]{mfcc3d.ps}](img102.png)
![\includegraphics[]{mfcc2d.ps}](img103.png)
![\includegraphics[]{empex.ps}](img104.png)

![\includegraphics[height=12cm]{mfccmarvin.ps}](img109.png)
![\includegraphics[]{empex.ps}](img104.png)
![\includegraphics[]{emp2.ps}](img110.png)
![\includegraphics[]{emp3.ps}](img111.png)
![\includegraphics[]{p3.ps}](img112.png)
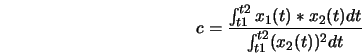


![]() , on obtient :
, on obtient :
![]() soient constituées
soient constituées

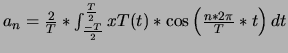



![]() pour n > 0
pour n > 0

![]() };
};
![]() } est :
} est :




![]() est infini.
Pour le résoudre:
on pose
est infini.
Pour le résoudre:
on pose
![]() avec N points entre 0 et 1.
avec N points entre 0 et 1.
![]() h= 0,1,2,3,...,N
h= 0,1,2,3,...,N




![]() est appelée transformée de Fourrier discrète (TFD), d'ordre N.
on peut représenter la TFD sous forme matricielle en mettant :
est appelée transformée de Fourrier discrète (TFD), d'ordre N.
on peut représenter la TFD sous forme matricielle en mettant :
![]()


![]() est pair, les carrés des n racines nièmes de l'unité sont les
est pair, les carrés des n racines nièmes de l'unité sont les ![]() racines
racines ![]() iemes de l'unité.
iemes de l'unité.


![]()
![]() longueur(A)
/* n est une puissance de 2 */
longueur(A)
/* n est une puissance de 2 */
![]() = 1
= 1
![]()
![]()
![]()
![]()
![]() 1
1
![]() { a(0) ; a(2) ; a(4) ; ... ; a(n-2) } /* tableau des valeurs d'indice pair de A */
{ a(0) ; a(2) ; a(4) ; ... ; a(n-2) } /* tableau des valeurs d'indice pair de A */
![]() { a(1) ; a(3) ; a(5) ; ... ; a(n-1) } /* tableau des valeurs d'indice impair de A */
{ a(1) ; a(3) ; a(5) ; ... ; a(n-1) } /* tableau des valeurs d'indice impair de A */
![]() FFT Recc(A[0])
FFT Recc(A[0])
![]() FFT Recc(A[1])
FFT Recc(A[1])
![]()
![]() 0 à
0 à ![]() - 1 faire
- 1 faire
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() Ainsi, nous avons au fur à mesure du signal une FFT
qui sera représentée ainsi :
Ainsi, nous avons au fur à mesure du signal une FFT
qui sera représentée ainsi :
![\includegraphics[]{spectre.ps}](img272.png)